Maurits Cornelis Escher nasce in Olanda a Leeuwarden il 17 giugno 1898, da una famiglia benestante, ultimo figlio dell'ingegnere George Arnold Escher e di Sara Gleichman.

Nel 1903 la famiglia si trasferisce a Arnhem, dove il giovane Maurits rivela scolasticamente un interesse saltuario e inadeguato per quasi tutte le discipline, eccezion fatta per il disegno al quale si dedica con sincero entusiasmo.

Dirà dei suoi docenti:

“Non una volta mi diedero una sufficienza in matematica. La cosa buffa è che, a quanto pare, io utilizzo teorie matematiche senza saperlo. Immaginatevi adesso che i matematici illustrano i loro libri con i miei quadri! Non riescono neppure a immaginarsi che io non ne capisco nulla”.

Il ragazzo, a vent’anni, consapevole delle proprie capacità, si iscrive all'Università Tecnica di Delft, incoraggiato dal padre che ne intuisce il talento artistico.

La lascia un anno dopo per la Scuola di Architettura e Arti Decorative di Haarlem, dove apprende i rudimenti dell'intaglio del legno. E’ qui che incontra il grafico Samuel Jessurun de Mesquita, affina il gusto estetico e scopre la passione per la xilografia. Nei suoi scritti dell’epoca rivela che può lavorare come un pazzo un giorno e non far nulla il successivo, andando su e giù per la stanza alla ricerca di una grande idea.

Rimane colpito dal suono emesso dall’organo della Cattedrale, dalle cui canne, ascoltando una fuga di Bach, gli pare di sentire tuonante la voce della Gloria Divina.

Nella primavera del 1922 visita l'Italia in compagnia di alcuni amici. I suoi occhi fissano la bellezza del paesaggio toscano. Gira il nostro paese, passando da Genova, Siena, e qui, colpito da tanta bellezza artistica, gli ritorna l’estro creativo ed esegue le prime incisioni lignee di paesaggi. Rimane piacevolmente colpito dalle città e dalle verdeggianti campagne toscane e affina la sua tecnica cercando di riprodurre accuratamente anche i dettagli del grandioso patrimonio naturalistico e artistico toscano.

Mosso da una crescente irrequietudine e dalla voglia di cambiare, Escher nella primavera del 1923 si trasferisce sulla costiera amalfitana e qui rimane colpito dalla suadente plasticità delle rocce calcaree a picco sul mare e, soprattutto, dalla commistione di elementi romani, greci e saraceni presenti nelle architetture di Ravello e Amalfi, città che lasciano un'impronta profonda nella sua fantasia.

Il soggiorno gli giova non solo artisticamente, ma anche sotto il profilo sentimentale: il pittore incontra il futuro amore della sua vita, Giulia Umiker detta "Jetta", figlia di un facoltoso banchiere svizzero, che dopo aver consolidato la sua fama dirigendo un'importante filiale di Mosca, era costretto a fuggire in seguito alla rivoluzione del 1917.

La Umiker, per di più, si interessa di pittura e di disegno: la scintilla amorosa non tarda a scoccare tra i due; si sposano nel 1924 a Viareggio e un anno dopo si stabiliscono a Roma. Sono anni felici, durante i quali Escher può finalmente dedicarsi con assoluta devozione alla sua vocazione grafica, senza per questo sacrificare la sua passione per i viaggi: in aprile, quando il clima mediterraneo arride ai viandanti, viaggia negli Abruzzi, in Campania, in Sicilia, in Corsica e a Malta.

Malgrado l'intensa attività grafica, il successo però tarda ad arrivare, e l’artista continua a dipendere dal sostegno finanziario dei genitori. Esher, nonostante ciò, vive anni idilliaci in Italia, che diviene per lui una seconda patria dove poter maturare tranquillamente la propria fisionomia artistica.

Negli anni Trenta, tuttavia, il Fascismo consolida il proprio potere: il clima politico teso e cupo è per lui insopportabile. Lascia l’Italia, trasferendosi con la famiglia in Svizzera; “in questo tremendo paesaggio misero e bianco” (per usare le sue parole) ci rimane un anno, come riporta Bruno Ernst:

“Il paesaggio non lo ispirava per nulla. Tenta di integrarsi con la comunità elvetica ma i monti sembravano pietraie senza storia, blocchi rocciosi senza vita”. L'architettura era asettica, era l'opposto dell'Italia meridionale, che tanto aveva catturato il suo sguardo. I tempi sono maturi per ritornare alla suadente mitezza del Mar Mediterraneo; così, invia una lettera alla Compagnia di Navigazione Adriatica, cui propone di pagare un viaggio andata e ritorno verso la Spagna meridionale con quarantotto stampe e quattro copie di dodici masselli. Le trattative vanno a buon fine e così, nel 1936, si imbarca con la moglie su un mercantile della compagnia Adriatica.

Il viaggio in Spagna è importante per la sua maturazione grafica: a Granada i mosaici dell'Alhambra, complesso moresco i cui interni sono ornati con motivi grafici ricorsivi, sono una fonte d'ispirazione.

In seguito, nel 1937 si trasferisce con la famiglia nella città belga di Uccle, nei pressi di Bruxelles: la seconda guerra mondiale è alle porte e l'artista vuole stare anche fisicamente più vicino ai suoi cari. Nel frattempo la sua arte subisce un drastico cambiamento tematico: Escher inizia a esplorare le sue visioni interiori. Nel 1941, complice anche il conflitto che insanguina il Belgio, Escher e la famiglia si spostano a Baarn; qui la sua notorietà si afferma e da questo momento la sua vita procede tranquilla: è un uomo felice, viaggia per il Mediterraneo. La sua alacre produttività si interrompe nel 1964, a causa di una grave malattia per cui è operato due volte. La lunga convalescenza mina la sua salute. Nel periodo successivo (dalla fine del 1968), la moglie si allontana e si trasferisce presso uno dei figli in Svizzera, dove muore poco dopo. Purtroppo le energie creative di Escher si esauriscono, sino a scomparire del tutto quando, nel 1970 si trasferisce a Laren, dove termina il suo viaggio terreno il 27 marzo 1972, all’età di quasi settantaquattro anni.

Ci chiediamo cosa ci è rimasto di Escher? Chi era? E come spiegare la rigorosa matrice matematico-geometrica della sua arte? Ai complimenti formulatigli nel 1966 dal musicista Graham Nash, circa le sue doti ricercate, replica di essere solo un matematico in cerca della rappresentazione della terza e quarta dimensione.

Escher con le sue opere è cantore di un mondo governato da armonie di tipo geometrico e matematico. “Mi sento spesso più vicino ai matematici che ai miei colleghi artisti” ammise Escher una volta, pienamente consapevole di come due mondi apparentemente distanti, come quelli dell'arte e della matematica, possono coesistere.

D’altronde gli anni in cui Escher approfondisce la propria maturazione artistica sono segnati da un profondo risveglio di fermenti culturali, decollati grazie allo slancio fornito dalle scoperte di Heisenberg ed Einstein, dalle esperienze estetiche del Surrealismo e del Cubismo, dai teoremi di Gödel e dai lavori di Turing.

Si afferma una scienza che, se da una parte fornisce all'uomo gli strumenti per conoscere e, dunque, dominare la Natura, dall'altra veicola anche profonde inquietudini e insicurezze che, come ebbe modo di asserire lo stesso Escher, aprono inesorabilmente pericolosi “sensi di vuoto”. Lo stesso Escher nella sua arte fa ricorso, consapevolmente o meno, a concetti matematici come le trasformazioni e la prospettiva nel piano cartesiano, sfiorando la geometria non euclidea (Poincaré).

Molte sue opere arrivano persino a preludere a principi scientifici che risultano assolutamente ignoti all'artista, essendo germogliati definitivamente solo molti decenni più tardi. Il fatto che la sua arte si strutturi su modelli geometrici e matematici ben precisi è tuttavia ancora più sorprendente alla luce delle sostanziali deficienze conoscitive dell'artista, del tutto alieno a quelle astrazioni matematiche che tanto appassionavano i professori nelle aule universitarie.

Escher inoltre è un artista molto sensibile alle suggestioni mistiche emanate dai cristalli e dai solidi platonici. I primi, infatti, sono porzioni di materia omogenea che rispondono a leggi geometriche costanti e, perciò, a forme poliedriche che appaiono perfette, misteriose e immutabili. Diceva l’artista: “Non sono creazioni della mente umana.” Semplicemente essi “sono”, esistono indipendentemente da noi.

In un attimo di lucidità, l'uomo può al più scoprire che esistono e rendersene conto. I poliedri regolari non sono invenzioni della mente umana, perché esistevano molto tempo prima che l’uomo comparisse sulla terra.

Questo interesse per i cristalli è rafforzato dalla collaborazione con il geologo Berend George, il quale pubblica nel 1935 un trattato sulla mineralogia generale e la cristallografia, che accende l'entusiasmo di Maurits Cornelis che esplora le potenzialità dei cristalli anche grazie alla conoscenza dei solidi platonici, così detti perché citati nel Timeo di Platone.

Questi sono poliedri caratterizzati da spigoli e angoli tutti uguali, considerati la massima espressione dell'armonia e della perfezione proprio in virtù della simmetria che li caratterizza (il tetraedro, il cubo, l'ottaedro, il dodecaedro e l'icosaedro).

Nelle sue opere Escher descrive una metodologia geometrica in grado di restituire una scomposizione ritmica del piano. Comprende che per piastrellare una superficie con un motivo ornamentale questo deve essere sottoposto a simmetria, traslazione, rotazione, riflessione.

Mondi e figure impossibili

Il nome di Escher è legato a quello dei “mondi impossibili”. Si tratta di una formulazione artistica degli stravolgimenti attuati da Albert Einstein con i suoi due postulati della teoria della relatività, i quali «richiedono l'abbandono della tradizionale concezione dello spazio e del tempo fondata sull'idea di un continuum spaziale fluente attraverso uno temporale, e conducono all'assunzione di un continuo spazio-temporale in cui distanze e spazi variano al mutare del sistema di riferimento» (Nicola Abbagnano).

Esaminiamo alcune opere esplicative dei concetti esposti e fondamentali nel cammino artistico dell’artista. In “Relatività” decide di registrare graficamente la paradossalità delle conquiste concettuali einsteiniane. Si tratta di una litografia che raffigura un universo relativistico, surreale, dove la percezione dei vari ambienti è affidata al punto di vista scelto dall'osservatore. Nello spazio illusorio della litografia sono infatti compresse le tre dimensioni spaziali tra loro ortogonali: le varie entità, possono essere interpretate in modi diversi a seconda della dimensione considerata (si può facilmente osservare, ad esempio, come ciò che in un mondo è una parete, in un altro è un soffitto, o magari un pavimento).

L'identificazione delle figure di “Relatività”, pertanto, cessa di essere un'operazione meccanica ed esige l'adozione di un punto di vista, soggettivo e relativo, da parte dell'osservatore: ecco, allora, che «ogni cosa appare del tutto normale se considerata localmente, ma è alquanto strana e surreale se considerata in rapporto al resto», per usare le parole di Gaetano Chiurazzi. Questa relativizzazione dello spazio pittorico culmina poi nelle scale, le cui alzate e pedate sono perfettamente interscambiabili. Sono moltissime, tuttavia, le rappresentazioni escheriane che, a dispetto della loro unitarietà, colgono simultaneamente più mondi distinti, sfidando la concettualità che da secoli si era sedimentata nella psiche umana.

Rilevante è una xilografia del 1956 (“Cigni”) ove gli uccelli volano in un cerchio chiuso fino a traslarsi nella loro immagine riflessa. Per farlo, devono sollevarsi dal piano e ribaltarsi di mezzo giro. Al centro i due gruppi cromatici a forma di otto sdraiato (o è l’infinito?) riempiono ogni spazio intersecandosi senza sovrapporsi.

Altra opera espressiva è “Sauri”, particolarmente interessante in quanto riunisce in maniera elegante i vari interessi che hanno animato le ricerche pittoriche di Escher. In questa litografia del 1943 sfruttando abilmente i pieni e i vuoti, vengono fatti corrispondere i profili di due creature, creando così un motivo replicabile all'infinito. Vi sono infatti raffigurati spazi dimensionalmente diversi dove alcune figure bianche e nere (qualificate da Escher come «ottimiste» e “pessimiste”) si distaccano dalla loro matrice tassellata e prendono vita.

Fortuna critica

Nonostante l'iniziale diffidenza dei critici, le opere grafiche di Maurits Cornelis Escher hanno raggiunto un successo planetario che non ha mai accennato a subire flessioni. Dapprima a riconoscere il valore dell'opera escheriana sono stati non tanto i critici d'arte, quanto i matematici e cristallografi, che per primi si sono interessati degli aspetti matematici delle litografie e si accorsero come Escher sia stato in realtà un’artista profondo e innovativo, in grado di vivacizzare gli schemi estetici del tempo. Il grafico Albert Flocon, ad esempio, nell'ottobre 1965 scrisse sulla rivista Jardin des Arts il seguente commento:

“La sua arte è sempre accompagnata da un'eccitazione passiva, dal brivido intellettuale di scoprirvi una struttura plausibile che contraddice la nostra esperienza quotidiana e la metta in discussione”

Questo giudizio di Flocon spianò la strada alla «Eschermania», in riferimento alla fanatica infatuazione che il pubblico ha dimostrato con il passare degli anni verso il grafico olandese. Sono stati molti i fattori a corroborare questo fenomeno: innanzitutto la vasta schiera di artisti dichiaratisi «discepoli» di Escher, (il pubblicitario David Hop, lo scultore Dominique Ribault, Lucio Saffaro e Hans Kuiper). Significative sono state le quantità di mostre d'arte a lui dedicate a partire da quella celeberrima tenutasi a L'Aia nel 1968 sino alle rassegne più recenti (Milano 2016-2017, Firenze 2021-2022) dove le opere in esposizione non sono subite passivamente dello spettatore, ma al contrario egli riveste un ruolo attivo con giochi didattici ed esperienze interattive che non solo ripropongono l'intimo carattere ludico distintivo delle opere escheriane, ma ne favoriscono anche un apprendimento, per così dire, «divertente».

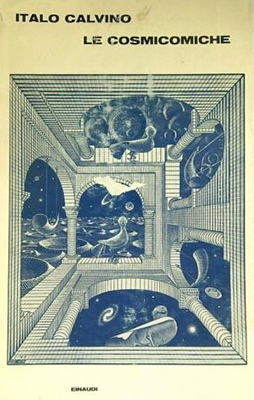
In questo modo l'arte di Escher si è diffusa nei biglietti d'auguri, nei francobolli, nelle scatole da regalo, nelle piastrelle dei pavimenti e nelle schede telefoniche, sino a impreziosire le copertine di illustri opere letterarie e musicali, come “On the Run” e “Ummagumma” dei Pink Floyd, e “Le cosmicomiche” di Italo Calvino.

Nel 1969 Mick Jagger, frontman dei Rolling Stones, scrisse ad Escher chiedendogli un'immagine inedita per la copertina dell'album “Through the Past Darkly”, ma questi rifiutò dicendo che aveva ben altro da fare, e concluse la missiva piccato per il tono confidenziale del cantante.

Esiste a Madrid un palazzo la cui facciata omaggia le metamorfosi escheriane.

Tutti, “dai matematici ai semplici curiosi, dai trasgressivi agli eccentrici, fino ai critici che vedono nell’opera di Escher un caso pressoché unico della creatività umana” (Marco Bussagli), hanno contribuito al riverbero di questa «Eschermania», che con lo sviluppo dei mezzi di comunicazione di massa è approdata anche nella cinematografia e nella fumettistica.

Un riferimento celebre, ad esempio, lo troviamo nella saga di Harry Potter, dove l'architettura della Scuola di Magia e Stregoneria di Hogwarts è movimentata da rampe di scale che cambiano magicamente posizione (“Tenete d'occhio le scale, a loro piace cambiare!” ricorda Percy Weasley ai nuovi condiscepoli, con un avvertimento denso di rimandi escheriani e moralistici).

L'aspetto angoscioso, surreale ed onirico delle opere di Escher viene ripreso anche nella locandina del film “Quella casa nel bosco”, negli spot pubblicitari della Audi A6 e della TIM, in una delle scene nodali di “Labyrinth - Dove tutto è possibile” di Jim Henson, e nella “Notte al museo - Il segreto del faraone” oltre che in alcuni episodi delle serie televisive de “ I Griffin”, “Futurama” e “I Simpson”. Il mai sopito interesse per le invenzioni di Escher viene poi testimoniato anche dai molteplici omaggi fumettistici provenienti, giusto per citarne alcuni, da Topolino, Martin Mystère e Dylan Dog.

Per concludere, Escher oltre che essere un incisore e grafico olandese è un matematico, che nella sua incapacità di prevedere, non aveva immaginato il successo delle sue stampe, specie tra le nuove generazioni.

Il suo nome è indissolubilmente legato alle sue litografie e stampe che tendono a presentare costruzioni impossibili, esplorazioni dell'infinito, tassellature del piano e dello spazio e motivi a geometrie interconnesse che mutano gradualmente in forme differenti. Le sue opere sono amate dagli scienziati, logici, matematici e fisici che apprezzano l’uso razionale dei poliedri, le distorsioni geometriche e le interpretazioni originali di concetti appartenenti alla scienza, portate a mete ed effetti paradossali.

Alessandro Blasi e Sergio De Benedictis
11-01-2023